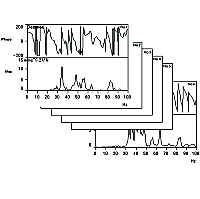
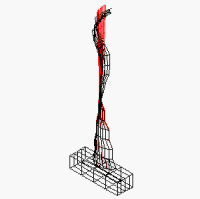
振動は、機械・構造物等に共通の問題です。この振動問題を解決するには、対象物の振動特性を正確に把握する必要がありますが、このためにはFEM等の理論解析とともに振動実験を実施することが不可欠です。
1.モード解析とは
振動の分野において「モード解析」とは、構造物の振動特性をモードの重ね合わせで表現する解析方法をさします。「モード」とは、「振動モード」または「振動形態」を意味します。例えば、図1に示す梁の曲げ振動の形態は、曲げ1次モード、曲げ2次モード、曲げ3次モードと呼ばれます。
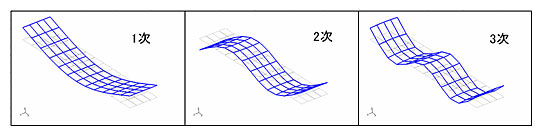
図1 自由支持された梁の固有モード
固有振動数、モード減衰比、固有モード(この場合有次元)の情報があれば、時刻歴応答や周波数応答などの任意の振動現象を必要最小限の自由度のモデルで表現できるため、計算効率が高い点がモード解析の特徴です。
2.モード解析の種類
モード解析は、理論モード解析と実験モード解析に大別されますが、最近では実験モード解析を応用した実稼動モード解析という解析手法も普及しつつあります。。
2-1 理論モード解析
「理論モード解析」は、FEMモデルでの固有値解析によるもので、理論モデルの質量行列と剛性行列から固有値問題を解いて固有値(固有振動数)と固有ベクトル(固有モード)を求める解析手法です。理論モード解析ではモード減衰比を求めることができません。
2-2 実験モード解析
「実験モード解析」は、加振試験によって求めた周波数応答関数、またはインパルス応答関数を曲線適合(*1)し、固有振動数、モード減衰比、固有モードを特定する解析手法で、一種のシステム同定といえます。実験モード解析で構築された実測によるモード解析モデルを用い、任意の振動現象を高い精度で表現することができます。
(*1)曲線適合:最小二乗近似によってモード解析理論に沿った関数を求めること
2-3 実稼動モード解析
「実稼動モード解析」は、構造物の固有振動数、モード減衰比、固有モードを振動応答のみから特定する解析手法です。ただし、実稼動モード解析によって得られる固有モードは無次元のものに限られます。
3.モード解析の適用範囲と適用例
3.1 理論モード解析の例
| 適用範囲 | モデル化可能なあらゆる構造物 |
|---|---|
| 適用例 | (1)時刻歴応答シミュレーション
※減衰が推定値であるため精度は保証されない (2)固有モードを参照した振動低減対策 ―構造変更による振動低減 ―動吸振器の設置位置の最適化 ―減衰付加位置の最適化 ―回転体における釣合わせ錘の取り付け面の最適化 |
図2は、梁構造物の固有値解析例です。左から1次、2次、3次、4次のモードです。この例では、2次モードが外力と共振する可能性があることが判明したため、横梁の剛性を上げる対策が行われました。
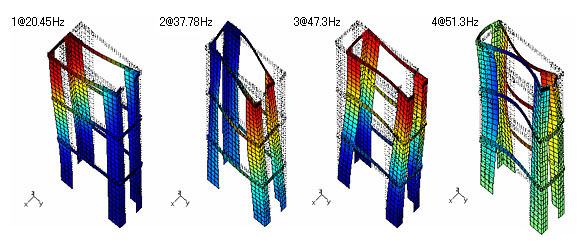
図2 梁構造物の固有値解析例
3.2 実験モード解析の例
| 適用範囲 | 加振試験の実施が可能な構造物 |
|---|---|
| 適用例 | (1)解析モデルの精度検証やチューニング
(2)固有モードを参照した振動低減対策 ―構造変更による振動低減 ―動吸振器の設置位置の最適化 ―減衰付加位置の最適化 (3)異常・損傷原因の特定 (4)可制御モデル(状態空間モデル)のシステム同定 (5)実験モード解析モデルによる時刻歴応答シミュレーション ※減衰が実測値であるため精度が保証される (6)実験モード解析モデルを応用した剛体特性(重心位置、主慣性モーメント、慣性主軸など)の計測 |
振動低減対策例
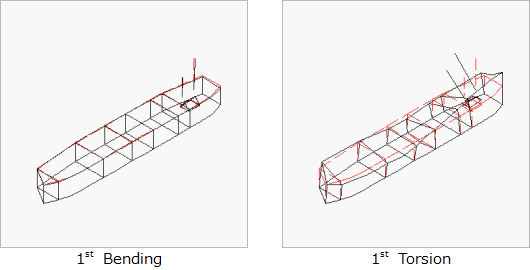
図3は、共通台板上に固定されたエンジンと減速機の実験モード解析例です。加振はインパルスハンマによって行われました。この例では、捩り1次モードが外力と近いことが判明したため、捩り剛性を上げる対策を行った結果、振動値が1/5以下に低減されました。
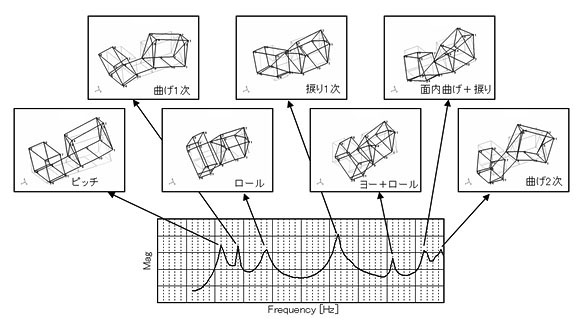
図3 共通台板上に固定されたエンジンと減速機の実験モード解析例
解析モデルの精度検証・チューニングの例
以下は、タービン翼を例として解析モデルの精度検証・チューニングのフローを示したものです。

|
|
| ↓ | |
|
|
| ↓ | |
|
|
| ↓ | |
|
|
| ↓ | |
|
その他の例
※下の画像をクリックすると、実際に得られた結果をアニメーションでご覧頂けます。
 図8 チタン製ギヤの音圧加振/ドップラー振動計測による事例
図8 チタン製ギヤの音圧加振/ドップラー振動計測による事例
3.3 実稼動モード解析例
| 適用範囲 | 加振試験の実施が困難な巨大構造物 |
|---|---|
| 適用例 |
|
図10は、鉄塔の実稼動モード解析例です。曲げ1次モードの固有振動数、モード減衰比、固有モードが実測によって確認されました。また、カルマン渦の発生周波数と曲げ1次モードの固有振動数が十分離れていることが確認されました。
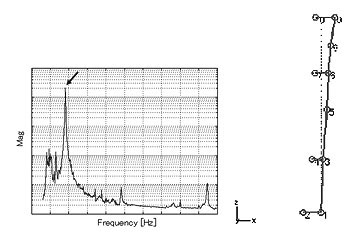 図10 鉄塔の実稼動モード解析例
図10 鉄塔の実稼動モード解析例
当社では、微少な薄膜から巨大な船舶・橋梁・鉄塔に至るまで、あらゆる構造物を対象とした、実験モード解析/実稼働モード解析に関する豊富な経験を有しています。また、材料評価やFEM解析などと合わせ、総合的に振動問題を解決する技術を提供しています。特に、実機の振動の「可視化」技術は大変ご好評をいただいております。
用語解説
振動特性
振動現象を表すために必要な情報です。「固有振動数」、「モード減衰比」、「固有モード」などがあります。固有振動数、モード減衰比、固有モードは、モードごとに決まった異なる値を持つため、固有という言葉で表現されます。
固有振動数
自由振動させたときの周波数で、単位は[Hz]です。 共振(外力の振動数と固有振動数が一致すること)が問題となる場合に非常に重要です。
モード減衰比
自由振動させたときの振動の収束性を示す値で、単位は無次元です。図A1に示す自由振動の場合、時間領域ではモード減衰比が大きいほど早く収束し、周波数領域ではモード減衰比が大きいほど振幅は小さくなります。共振時の振幅は、モード減衰比が大きいほど小さくなります。
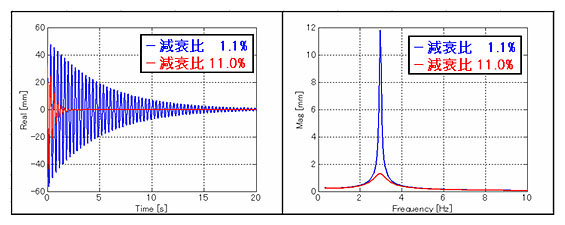 図A1 自由振動の波形(左)とスペクトル(右)
図A1 自由振動の波形(左)とスペクトル(右)
固有モード
自由振動させたときの振動形態/振動形状で(図1参照)、単位は、[m/N]、[(m/s)/N]、[(m/s2)/N](それぞれ単位力あたりの振動変位、振動速度、振動加速度)で表されます。固有モードは比率だけでも表現できるため、無次元で表示することもできます。最大振幅や単位モード質量で正規化することもできます。
モードの重ね合わせ
モードごとの振動応答の線形和です。任意の点で観測される振動応答はその点の個々のモードの振動応答の重ね合わせで表現されます。これは、時間領域と周波数領域のどちらでも成り立ちます(図A2および図A3参照)。
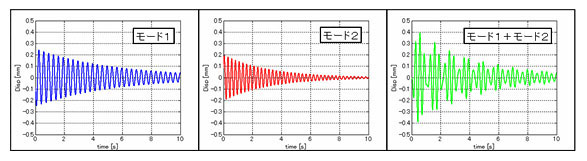 図A2 2自由度系におけるモードの重ね合わせの例(時間領域)
図A2 2自由度系におけるモードの重ね合わせの例(時間領域)
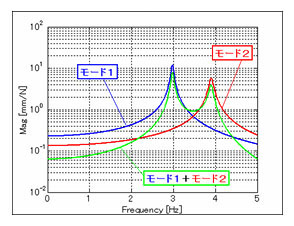 図A3 2自由度系におけるモードの重ね合わせの例(周波数領域)
図A3 2自由度系におけるモードの重ね合わせの例(周波数領域)